Study hard
(c++)백준 15685번: 드래곤 커브 본문
15685번: 드래곤 커브
첫째 줄에 드래곤 커브의 개수 N(1 ≤ N ≤ 20)이 주어진다. 둘째 줄부터 N개의 줄에는 드래곤 커브의 정보가 주어진다. 드래곤 커브의 정보는 네 정수 x, y, d, g로 이루어져 있다. x와 y는 드래곤 커
www.acmicpc.net



[풀이]
처음 문제를 봤을 때 참 난감한 문제였다.. 시뮬레이션 구현 문제는 규칙이 있기 마련이기에 손으로 그려보면서 규칙을 찾았다.
먼저 각 방향이 다음세대를 그릴 때 어떻게 바뀌는지 찾았다.
방향은 아래와 같이 바뀐다.
0 → 1 (→ ↑)
1 → 2 (↑ ←)
2 → 3 (← ↓)
3 → 0 (↓ →)
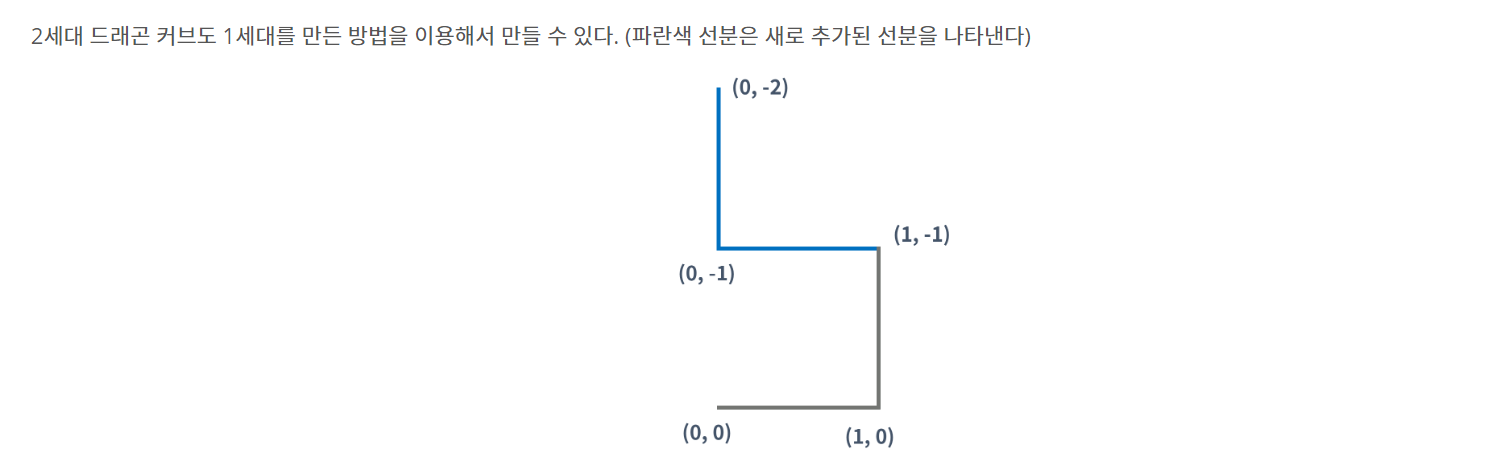
그리고 다음세대에 새로 그려지는 드래곤 커브가 어떤 순서로 그려지는 지 찾았다. 앞세대의 드래곤 커브를 복사하여 끝 부분에 붙인다고 했을 때, 앞 세대에서 가장 마지막에 그려진 것부터 역순으로 그려진다.
아래 그림과 같이 대응된다.

위의 규칙들을 따라서 드래곤 커브를 그릴때마다 그 방향들을 다음세대를 위해 저장하고, 다음 세대를 그릴 때 가장 마지막에 저장된 방향부터 방향 규칙에 따라 변경후 드래곤 커브를 그려주면 된다.
#include <iostream>
#include <vector>
using namespace std;
int N;
int Grid[101][101] = { 0, };
const int dxy[][2] = { {0,1},{-1,0},{0,-1},{1,0} };//0:오른쪽, 1:위, 2:왼쪽, 3:아래
int convert[] = { 1,2,3,0 };
vector<int>dir;
void DragonCurve(int cnt, int g, int x, int y) {
if (cnt == g + 1) {
return;
}
int nx = x;
int ny = y;
int dir_size = dir.size();
for (int d = dir_size - 1; d >= 0; d--) {
int nd = convert[dir[d]];
nx += dxy[nd][0];
ny += dxy[nd][1];
dir.push_back(nd);//다음 세대 위해 현재 방향 정보 저장
Grid[nx][ny] = 1;//드래곤 커브 지나감
}
DragonCurve(cnt + 1, g, nx, ny);
}
int getSquare() {
int cnt = 0;
/*
cout << '\n';
for (int i = 0; i < 10; i++) {
for (int j = 0; j < 10; j++) {
cout << Grid[i][j] << ' ';
}
cout << '\n';
}
*/
for (int i = 0; i < 100; i++) {
for (int j = 0; j < 100; j++) {
if (Grid[i][j] == 1 && Grid[i][j + 1] == 1 && Grid[i + 1][j] == 1 && Grid[i + 1][j + 1] == 1)
cnt++;
}
}
return cnt;
}
int main() {
cin >> N;
int x, y, d, g;
while (N--) {
dir.clear();
cin >> y >> x >> d >> g;
//0세대 미리 해주기(두 칸 칠해줘야 하므로!)
Grid[x][y] = 1;
x += dxy[d][0];
y += dxy[d][1];
Grid[x][y] = 1;
if (g == 0)
continue;
dir.push_back(d);
//1세대부터 시작
DragonCurve(1, g, x, y);
}
cout << getSquare() << '\n';
return 0;
}'백준 > 시뮬레이션,구현' 카테고리의 다른 글
| (C++)백준 20061번: 모노미노도미노 2 (0) | 2021.04.21 |
|---|---|
| (c++)백준 15686번: 치킨 배달 (0) | 2021.04.10 |
| (c++)백준 14891번: 톱니바퀴 (0) | 2021.04.05 |
| (c++)백준 14890번: 경사로 (0) | 2021.04.04 |
| (c++)백준 20058번: 마법사 상어와 파이어스톰 (0) | 2021.03.27 |




